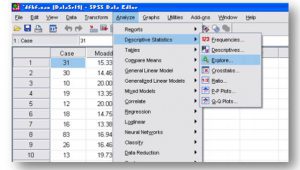
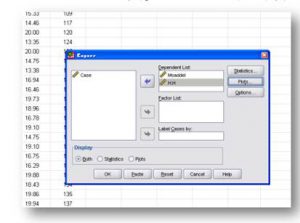
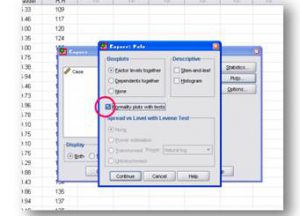
زیر منوی Descriptive Statistics شامل گزینه های Frequencies , Descriptives , Explore ,Crosstabs Ratio، است. اغلب پژوهش ها نیاز به استفاده از تمامی این گزینه ها دارند توصیه می شود در یادگیری آن ها بیشتر دقت شود.
آموزش منوی Frequencies
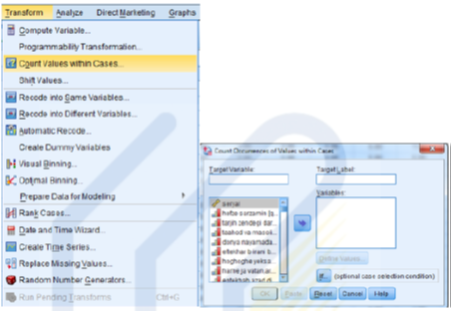
برای به دست آوردن جدول فراوانی از منوی Frequencies استفاده می شود.
مراحل اجراء منوی Frequencies

 ?
?
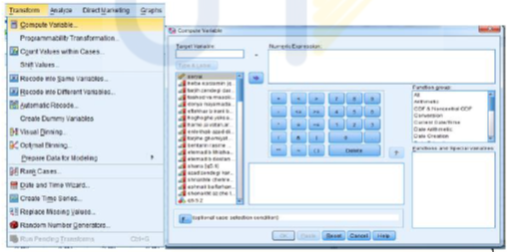
اولین مرحله در تجزیه و تحلیل داده ها جداول یک بعدی است. جداول یک بعدی برای همه متغیرهای اسمی، ترتیبی و فاصله ای قابل اجراء و ترسیم است. منتهی برای متغیرهای فاصله ای و نسبی به خصوص تعداد مقوله های گسترده باشد چندان تحلیل مناسب ارائه نمی دهد، در این گونه موارد باید از آمارهای توصیفی کمک گرفت. (در شکل زیر به طور تفصیلی اجرای منوی Frequencies ارائه شده است)
باکس Frequencies
1- مستطیل لیست متغیرها:
محل نشان دادن متغیرها همراه با سطح سنجش متغیرها است.
2- محل متغیرهای مورد بررسی (variables):
در این مرحله پژوهشگر متغیر مورد نظر را برای تجزیه و تحلیل انتخاب و سپس روی فلش کلیک می کند تا متغیر برای تجزیه و تحلیل به محل خود انتقال یابد.
3- بخش آماره statistics: شامل چهار موضوع اساسی مجموعه درصد ها Percentiles، آماره های گرایش مرکزی Central Tendency، پراکندگی Dispersion و توزیع Distribution است.
1- مجموعه درصد ها Percentiles: شامل چارک ها، دهک ها و درصد ها مورد نیاز می باشد.
2- آماره های گراسش مرکزی Central Tendency: شامل سه آماره میانگین، میانه، مد و مجموع می باشد.
3- پراکندگی Dispersion: شامل واریانس، انحراف معیار، دامنه تغییرات، منیمم، ماکسیمم و خطای استاندارد میانگین.
4- توزیع Distribution: شامل چولگی و کشیدگی می باشد.

 ?
?
چندک ها (Quantiles)
مقادیری از مشاهدات هستند که دامنه تغییرات را به فاصله های چندکی مورد نیاز تقسیم می کنند، به طوری که فراوانی در هر یک از این فواصل، درصد معینی از فراوانی کل را تشکیل می دهند. بنابراین، اگر دامنه تغییرات را به چهار قسمت مساوی تقسیم کنیم، به چارک ها (Quartiles)، اگر به ده قسمت مساوی تقسیم کنیم، به دهک ها (Deciles)، و اگر به صد قسمت مساوی تقسیم کنیم، به صدک ها (Percentiles) دست پیدا می کنیم.
چارک ها (Quartiles)
چارک ها نقاطی بر روی مقیاس اندازه گیری هستند که کلیه مشاهدات و نمره ها را به چهار قسمت مساوی (برابر با میانه بوده و از طریق تفاضل چارک ها اول از چارک سوم به دست می آید. در واقع، میانه، چارک دوم) نقطه ای است که 75 درصد نمرات (معادل سه چهارم) در پایین یا مساوی آن واقع شده اند. هر چه مقدار انحراف چارکی بیشتر باشد، پراکندگی نمرات از میانه بیشتر است.
همانند شاخص های گرایش مرکزی، شاخص های پراکندگی برای توصیف و خلاصه کردن توزیع نمرات استفاده می شود. شاخص های پراکندگی، چگونگی گسترش و پراکندگی مقادیر یک توزیع را نشان می دهند.
شاخص های پراکندگی اطلاعات ارزشمندی در مورد توزیع نمرات به ما می دهند.
نما یا مد (Mode)
نما، که آن را با علامت MO نمایش می دهند، عبارت است از طبقه، وضعیت و یا عددی که با توجه به متغیر مورد نظر، بیش ترین پاسخ گویان (پاسخ ها) را به خود اختصاص داده است. این شاخص برای تمامی متغیرهای اسمی، ترتیبی، فاصله ای و نسبی استفاده می شود.
میانه (Median)
میانه، که آن را علامت Md نشان می دهند، عبارت است از طبقه، وضعیت و یا عددی که پاسخ گویان را با توجه به متغیر مورد نظر، به دو گروه مساوی تقسیم می کند و تقریباً نیمی از داده ها از آن کمتر و نیمی دیگر از آن بیشتر هستند.
میانگین یا میانگین حسابی (Mean or Arithmetic Mean)
نشان می دهند، به عنوان اصلی ترین شاخص گرایش به مرکز محسوب می شود که عبارت می باشد از متوسط نمرات پاسخ گویان در متغیر مورد نظر. یعنی مجموع نمرات یا مقادیر تقسیم بر تعداد آن.
نکات:
نشان می دهند.
شاخص میانگین عموماً برای متغیرهای با مقیاس فاصله ای و نسبی به کار می رود. البته گاهی در تحقیقات اقتصادی و اجتماعی نیز از این شاخص برای مقایسه توزیع نمرات در بین چندین سوال یا گویه و در نتیجه توضیح بهتر نتایج فراوانی و درصدی در بین این سوالات و گویه ها استفاده می شود.
– در هنگام محاسبه میانگین، در صورتی که داده های پرت در میان مجموع داده ها باشد، باید داده های پرت را حذف و یا معادل با بالاترین و یا کم ترین عدد قرار دهیم. برای مثال، اگر در یک جامعه طیف درآمدی بین 100 تا 700 هزار تومان باشد، اگر چند نفری دارای درآمد بالای 700 هزار تومان باشند، می توانیم با استفاده از دستور Recode اعداد فوق را به حداکثر داده ها تبدیل کرده و یا این که حذف می کنیم.
دامنه تغییرات (Range)
دامنه تغییرات ساده ترین شاخص پراکندگی است و فقط به تفاضل بین بیشترین و کمترین نمرات در توزیع اشاره دارد. علی رغم سادگی محاسبه دامنه تغییرات،این شاخص فقط برای داده های فاصله ای و نسبی مناسب است. در عمل تفاضل مورد استفاده برای به دست آوردن دامنه تغییرات، فرض می شود مقادیر نمرات در یک توزیع معنی دار هستند. این نکته فقط در مورد داده های سطح فاصله ای و نسبی صدق می کند.
واریانس (Variance)
واریانس به میزان تفاوت و پراکندگی پاسخ گویان از مقادیر میانگین اشاره دارد. به عبارتی واریانس یک شاخص پراکندگی است که از طریق محاسبه انحراف نمره ها از میانگین محاسبه می شود و عبارت است از میانگین انحراف از نمره ها از میانگین یا مجموعه مجذورات انحراف نمره ها از میانگین تقسیم بر تعداد نمره ها واریانس نشان می دهند.
انحراف استاندارد (Standard Deviation = SD)
انحراف استاندارد نیز، همانند واریانس به پراکنش پاسخ گویان در اطراف میانگین راجع است. انحراف استاندارد که جذر واریانس می باشد شاخصی است که متوسط پراکندگی نمرات از میانگین را نشان می دهد و لذا اغلب همراه با میانگین گزارش می شود. تفسیر مقدار انحراف استاندارد بدین صورت است که هر چه مقدار انحراف استاندارد بیشتر باشد، پراکندگی نمرات از میانگین هم بیشتر است. یعنی گروه مورد مطالعه از لحاظ ویژگی مورد سنجش نا متجانس تر است و بر عکس، مقدار کوچک انحراف استاندارد بیان گر تجانس بیشتر گروه از لحاظ ویژگی مورد سنجش است.
چولگی (Skewness)
شاخص چولگی که به شاخص انحراف از قرینگی نیز معروف است، میزان تقارن یک توزیع را اندازه گیری می کند. ضریب چولگی بین 3- و 3+ تغییر می کند و در عمل به ندرت به حد خود نزدیک می شود. چولگی می تواند به سه شکل مثبت، منفی و صفر اتفاق بیافتد:
چولگی مثبت: نشان گر آن اسن که توزیع داده ها و منحنی آن به گونه ای مثبت به صورت چوله در آمده است.
یعنی نمرات افراد حول و حوش مقادیر بالای متغیر متمرکز اند.
چولگی صفر: نشان دهنده آن است که توزیع داده ها متقارن است.
در کل هر چه مقدار چولگی بزرگ تر (معمولاً بزرگ تر از یک) باشد، در آن صورت نتیجه می گیریم که توزیع داده ها تفاوت فاحشی با توزیع متقارن دارد.
کشیدگی (Kurtosis)
کشیدگی نمایانگر میزان تفاوت توزیع پاسخ گویان از توزیع نرمال می باشند. این آماره نشان می دهد که آیا مقدیر توزیع پاسخ گویان بزرگ تر از میانگین است یا کوچک تر از آن. شاخص کشیدگی یکی از آماره های مناسب برای مقایسه پراکندگی توزیع جامعه با توزیع نرمال است. توزیع داده ها با توجه به مقدار کشیدگی می تواند به سه شکل باشد:
کشیدگی مثبت: نشانگر آن است که توزیع داده ها از توزیع نرمال بلند تر است. در چنین حالتی، توزیع داده ها حول میانگین متمرکز شده و از پراکندگی کمتری برخوردار است.
کشیدگی منفی: نشان می دهد که توزیع داده ها از توزیع نرمال کوتاه تر است. در چنین حالتی، توزیع داده ها در اطراف میانگین پخش شده و از پراکندگی زیادی برخوردار است.
کشیدگی صفر: نشان دهنده آن است که توزیع داده ها متقارن است. یعنی مقدار کشیدگی داده ها با مقدار کشیدگی توزیع نرمال کاملاً مساوی است.
در کل هر چه مقدار کشیدگی بزرگ تر (معمولاً بزرگ تر از یک) باشد، در آن صورت نتیجه می گیریم که توزیع داده ها تفاوت فاحشی با توزیع نرمال دارد.
نکات:
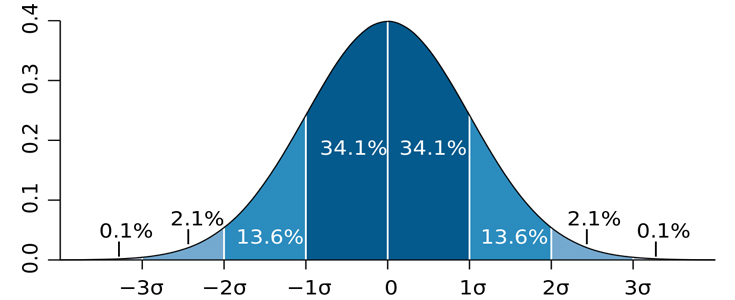
منحنی توزیع نرمال، بهترین نمایش برای انواع شاخص های گرایش به مرکز و گرایش به پراکندگی می باشد. منحنی نرمال، میزان تفاوت توزیع پاسخ گویان از توزیع نزمال را نشان می دهد که نقطه اوج آن، مقدار میانگین است.
از آنجا که بسیاری از آزمون های آماری بر این فرض اند که داده ها به صورت نرمال توزیع شده اند، بنابراین چک کردن توزیع داده ها از طریق مقادیر چولگی و کشیدگی ایده خوبی است. همچنین، در صورتی که داده ها به صورت نرمال توزیع نشده اند، می توان از تغییرات لازم و یا آزمون های ناپارامتری متناسب استفاده کرد.
نمودار (Chart)
شامل نمودار میله ای، دایره ای و هیستوگرام می باشد.

 ?
?
فرمت Format: شامل مرتب کردن «صعودی (Ascending Values) و نزولی (Descending Values)» داده ها بر اساس کدهای متغیر و مرتب کردن داده ها به صورت «صعودی (Ascending Counts) و نزولی (Descending Values)» بر اساس فراوانی کدهای متغیر می باشد.

 ?
?
09357258425
www.pajuha.ir
info@pajuha.ir
سفارش ترجمه تخصصی